1936. Flights
The Chief
Engineer Peter was asked to develop a new model of aircraft for the company
“Air Bubundiya”. It was found that the hardest part is choosing the optimal
size of the fuel tank.
The Chief
Cartographer of “Air Bubundiya” John has made a detailed map of Bubundiya. On
this map he marked the fuel consumption for the flight between each pair of
cities.
Peter wants
to make the size of fuel tank as small as possible, so that the aircraft can
fly from any city to any other (possibly with refueling in cities on the way).
Input. The first line contains the number
of cities n (1 ≤ n ≤ 1000) in Burbundiya. Each of
the next n lines contains n numbers. The j-th number in the i-th
line equals to fuel consumption during the flight from i-th city to the j-th.
All numbers are nonnegative and less than 109. It is known that for
any i the number at the i-th line and the i-th position is zero.
Output. Print one number – the optimal size of the
fuel tank.
|
Smple input |
Sample output |
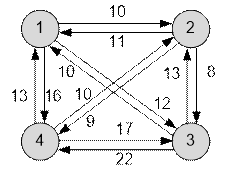
40 10 12 1611 0 8 910 13 0 22
13 10
17 0 |
10 |
SOLUTION
graphs – strongly connected components
Algorithm analysis
Let the tank
size be x. Construct a graph
in which there is a directed edge (i, j) if and only if the amount of fuel
required for a direct flight from the i-th city
to the j-th city is no
more than x (that is, with
the available tank, you can make a direct flight).
You can fly from
any city to any one only if the graph is strongly connected. Instead of
calculating the number of strongly connected components, we will use the
following property.
Graph is strongly
connected if the following statements hold for any vertex v:
·
from the vertex v there is a path to all the other vertices;
·
from any vertex there is a path to v;
Moreover, if
these statements are true for at least one vertex v, then they are true for all other vertices. These properties can
be checked by running a depth first search on a graph, for example, from a zero vertex
(for definiteness, the vertices are numbered from 0 to n – 1).
Thus, for a tank
of size x, we have
learned to determine whether an airplane can get from any city to any other. It
remains to find the required minimum possible volume of the aircraft tank using
the binary search method.
Example
Graph, given in a sample, has the form:
On the left
side, presented a graph
of possible flights with a tank volume of 9, and on the right with a volume of 10.
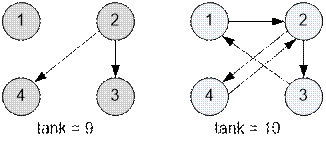
With a tank of size 10, an
airplane can fly from any city to any other.
Algorithm realization
Store the matrix
of fuel consumption between cities in the array graph. The array used
is used to mark the already visited vertices.
#define MAX 1010
int graph[MAX][MAX], g[MAX][MAX];
int used[MAX];
Start the function dfs of depth first search from
the vertex v. If type
= 0, then
go along the edges according to their direction. When type = 1,
depth first
search is performed along the edges in the opposite direction.
void dfs(int
v, int type)
{
used[v] = 1;
for(int i = 0; i < n; i++)
if ((type ?
g[i][v] : g[v][i]) && !used[i]) dfs(i,type);
}
The function AllVisited checks
if all the edges of the graph are visited during the depth first search. The answer will be positive and the function will return 1
if all cells of the array used contain
one.
int AllVisited(void)
{
for(int i = 0; i < n; i++)
if
(!used[i]) return 0;
return 1;
}
The main part of
the program. Read the
input fuel consumption matrix into the array graph.
scanf("%d",&n);
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
scanf("%d",&graph[i][j]);
Find the minimum tank
size using binary search on a segment [L; R]. Initially set [L; R] = [0; 2000000000].
L = 0; R =
2000000000;
while(L < R)
{
Mid = (L + R) / 2;
At each
iteration of the binary search, construct the adjacency matrix g of the directed graph: g[i][ j]
= 1, if a direct flight with tank volume Mid can be made from city i
to city j.
for(i = 0; i
< n; i++)
for(j = 0; j
< n; j++)
g[i][j] = (graph[i][j] <= Mid);
Start depth first search from the zero vertex. If all the other vertices can be reached from zero vertex, and zero vertex can be reached from all the other vertices, then graph
is strongly connected. In this case, the value of the variable flag remains 0.
memset(used,0,sizeof(used));
dfs(0,0); flag = 0;
if
(AllVisited())
{
memset(used,0,sizeof(used));
dfs(0,1);
if
(!AllVisited()) flag = 1;
} else flag =
1;
Recompute the boundaries of the binary search interval depending on
the value of flag.
if (!flag) R
= Mid; else L = Mid + 1;
}
Print the required
minimum tank size L.
printf("%d\n",L);
Java realization
import java.util.*;
public class Main
{
static int graph[][];
static boolean g[][], used[];
static int n;
//type = 0
original edges
//type = 1
reversed edges
static void dfs(int v, int type)
{
used[v] = true;
for(int i = 0; i < n; i++)
if ((type == 1 ? g[i][v] : g[v][i]) && !used[i]) dfs(i,type);
}
static boolean AllVisited()
{
for(int i = 0; i < n; i++)
if (!used[i]) return false;
return true;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
graph = new int[n][n];
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
graph[i][j] = con.nextInt();
g = new boolean[n][n];
used = new boolean[n];
int L = 0, R = Integer.MAX_VALUE;
while(L < R)
{
int Mid = (L + R) / 2;
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
g[i][j] = (graph[i][j] <= Mid);
Arrays.fill(used, false);
dfs(0,0);
boolean flag = false;
if (AllVisited())
{
Arrays.fill(used, false);
dfs(0,1);
if (!AllVisited())
flag = true;
} else flag = true;
if (flag == false) R = Mid; else L = Mid + 1;
}
System.out.println(L);
con.close();
}
}